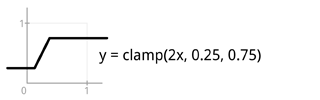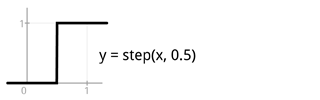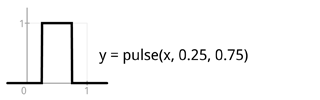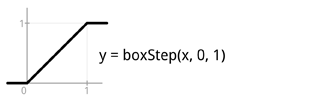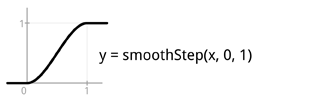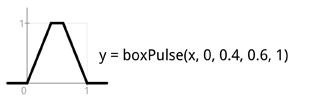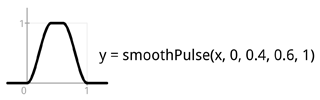A few years ago I read the book Texturing and Modeling: A Procedural Approach (Ebert et al.) and found some low level “step” and “pulse” primitives used for generating procedural graphics. It didn’t take a long time to notice that those are actually really useful in many other situations as well.
A generic pattern is that some value changes its value from a to b over t iterations, and you want something other to move along from c to d in the same time. Implementation is easier when the transition from a to b is just normalized to [0..1]. After that it’s really easy to map it to any range just by another multiplication (d – c) and adding an offset (c).
The “boxStep” function does the normalization part described above. However, just linear movement is actually quite boring, so the funky part here is that you can just switch “boxStep” to a “smoothStep” and there we go, movement along a smooth curve which feels better. Or you can map the boxStep result to a different function which takes in a value in the [0..1] range and outputs a value in the same range, e.g. sqrt().
Here’s a reference of the few basic such primitives, starting from the very basic clamp and step which are used to build the others. Including a header file to be used with C source. Works also when copy-pasted into Java. I rendered the images below using Processing, outputting result into a PDF file. Source code of that is also included below.
Download .h header file for C/C++
Download above graphs as a .pdf file
Download Processing .pde source file for creating the pdf
Since the roots of these functions are still in the procedural graphics, you can naturally spot this stuff in the modern shading languages, for example there’s smoothStep() available in GLSL (note that order of the arguments differs).
For more related information, check out Sol’s Interpolation tutorial (don’t forget to check his list of further references down the page).